隨(sui)機(ji)變量模(mo)型(xing)和(he)隨(sui)機(ji)過程模(mo)型(xing)是研究高清下載香蕉視頻app蘋果:應力腐蝕概率的(de)常(chang)用模(mo)型，本章(zhang)重(zhong)點介紹隨機(ji)變量(liang)模(mo)型。

一、應力-強(qiang)度干涉模型

 1942年，Pugsley提出了采用應力、強(qiang)度(du)分(fen)布函數曲線的(de)(de)(de)干涉(she)區面積分(fen)析(xi)失效概(gai)率的(de)(de)(de)方法，即應力－強(qiang)度(du)干涉(she)模型(xing)，該模型(xing)在構(gou)件和系(xi)統(tong)的(de)(de)(de)可靠性分(fen)析(xi)中得到了廣(guang)泛應用。目前(qian)，已(yi)成為分(fen)析(xi)構(gou)件和系(xi)統(tong)失效概(gai)率的(de)(de)(de)重要模型(xing)之一(yi)。在結(jie)(jie)構(gou)可靠性分(fen)析(xi)中，應力－強(qiang)度(du)（S-R)干涉(she)模型(xing)應用最廣(guang)，模型(xing)中的(de)(de)(de)S和R的(de)(de)(de)含義不僅僅是(shi)力學分(fen)析(xi)中的(de)(de)(de)應力和強(qiang)度(du)，二者具有更廣(guang)泛的(de)(de)(de)范疇(chou)。對于一(yi)個系(xi)統(tong)而言，S指的(de)(de)(de)是(shi)造成結(jie)(jie)構(gou)破(po)壞(huai)的(de)(de)(de)所有因素，即推動力；R代表了結(jie)(jie)構(gou)抵抗(kang)(kang)破(po)壞(huai)的(de)(de)(de)能(neng)力，即阻(zu)抗(kang)(kang)力。

  應(ying)(ying)力(li)(li)(li)腐(fu)(fu)(fu)蝕(shi)(shi)斷裂(lie)是(shi)一種低(di)應(ying)(ying)力(li)(li)(li)脆斷，是(shi)斷裂(lie)和腐(fu)(fu)(fu)蝕(shi)(shi)兩種機理相互影響(xiang)的(de)(de)結(jie)果。因此，當應(ying)(ying)力(li)(li)(li)還遠低(di)于斷裂(lie)應(ying)(ying)力(li)(li)(li)時(shi)就(jiu)能(neng)引起應(ying)(ying)力(li)(li)(li)腐(fu)(fu)(fu)蝕(shi)(shi)裂(lie)紋的(de)(de)產生(sheng)和擴(kuo)展(zhan)。應(ying)(ying)力(li)(li)(li)作(zuo)用降低(di)了材(cai)料的(de)(de)耐腐(fu)(fu)(fu)蝕(shi)(shi)性能(neng)，而腐(fu)(fu)(fu)蝕(shi)(shi)降低(di)了材(cai)料的(de)(de)斷裂(lie)強度，兩者是(shi)互相促進(jin)的(de)(de)。也就(jiu)是(shi)說，機械(xie)力(li)(li)(li)和化學力(li)(li)(li)的(de)(de)協(xie)同作(zuo)用導致了裂(lie)紋的(de)(de)擴(kuo)展(zhan)，如(ru)果只有應(ying)(ying)力(li)(li)(li)或腐(fu)(fu)(fu)蝕(shi)(shi)單獨作(zuo)用，是(shi)不會(hui)出(chu)現應(ying)(ying)力(li)(li)(li)腐(fu)(fu)(fu)蝕(shi)(shi)斷裂(lie)的(de)(de)結(jie)果。應(ying)(ying)力(li)(li)(li)腐(fu)(fu)(fu)蝕(shi)(shi)斷裂(lie)要經過(guo)一定的(de)(de)時(shi)間才能(neng)發(fa)生(sheng)，這是(shi)因為能(neng)量積(ji)蓄到使(shi)材(cai)料破壞的(de)(de)程(cheng)度是(shi)需要時(shi)間的(de)(de)，應(ying)(ying)力(li)(li)(li)腐(fu)(fu)(fu)蝕(shi)(shi)是(shi)使(shi)材(cai)料強度逐漸退化的(de)(de)過(guo)程(cheng)，因此，我(wo)們可以(yi)采用耐久(jiu)性損傷模(mo)型來描述應(ying)(ying)力(li)(li)(li)腐(fu)(fu)(fu)蝕(shi)(shi)失效的(de)(de)物理過(guo)程(cheng)。由(you)S-R干涉模(mo)型的(de)(de)理論可以(yi)寫出(chu)結(jie)構(gou)的(de)(de)極限狀態(tai)方程(cheng)

  因此，對于(yu)(yu)失效概(gai)率的(de)研究就轉化為對強度和(he)應力由于(yu)(yu)概(gai)率分布(bu)干涉引(yin)起的(de)狀態(tai)失效問題的(de)研究。當fs(s)和(he)fR(r)分別表示應力和(he)強度的(de)概(gai)率密度函數時，圖中(zhong)兩者重疊部分面積反映了失效概(gai)率的(de)大小，如圖6-1所示。

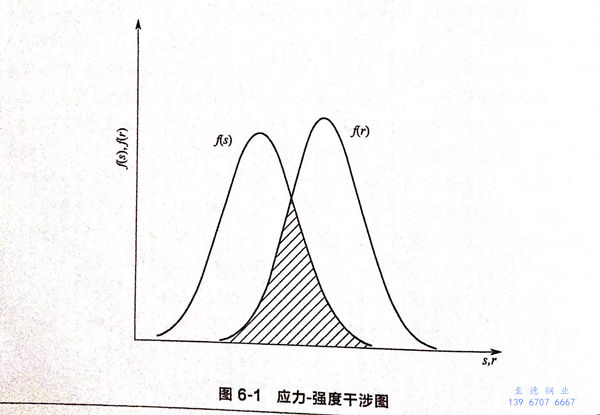
  假如最初應力(li)(li)與強度(du)是留有充分(fen)的(de)(de)安(an)全余量的(de)(de)，那么(me)經(jing)過一定時間后(hou)，隨著(zhu)應力(li)(li)分(fen)布(bu)與強度(du)分(fen)布(bu)的(de)(de)交疊，就有失(shi)效發生，這種(zhong)情形(xing)可以說是耐(nai)久模型(xing)的(de)(de)典型(xing)例子。根據(ju)應力(li)(li)－強度(du)干(gan)涉模型(xing)不但能夠求解應力(li)(li)腐蝕失(shi)效概(gai)(gai)(gai)率，還(huan)可以分(fen)析應力(li)(li)腐蝕不同階段(duan)的(de)(de)概(gai)(gai)(gai)率情況，如裂紋(wen)的(de)(de)萌(meng)生概(gai)(gai)(gai)率、裂紋(wen)的(de)(de)擴展概(gai)(gai)(gai)率等。

  當材(cai)料發生腐蝕(shi)后，隨著(zhu)時(shi)(shi)間(jian)的(de)推移，材(cai)料抵抗破壞的(de)能力(li)(li)降低(di)，而(er)腐蝕(shi)環境很可能變得更加(jia)苛刻。例如應力(li)(li)腐蝕(shi)，隨著(zhu)裂(lie)紋(wen)的(de)擴展，材(cai)料強度降低(di)、裂(lie)紋(wen)尖端應力(li)(li)集(ji)中(zhong)區域增大(da)，局部(bu)存(cun)在侵蝕(shi)性離子的(de)富集(ji)，使得廣義應力(li)(li)變大(da)而(er)強度降低(di)，此時(shi)(shi)S(t)和R(t)都是與時(shi)(shi)間(jian)有關(guan)的(de)變量(liang)，很顯然，概率密(mi)度函數也(ye)著(zhu)時(shi)(shi)間(jian)的(de)變化(hua)(hua)而(er)變化(hua)(hua)。當強度隨時(shi)(shi)間(jian)發生衰(shuai)退時(shi)(shi)，強度和應力(li)(li)組(zu)成的(de)干涉區域隨時(shi)(shi)間(jian)變化(hua)(hua)會越來越大(da)，這意味著(zhu)產品可靠(kao)性在降低(di)。

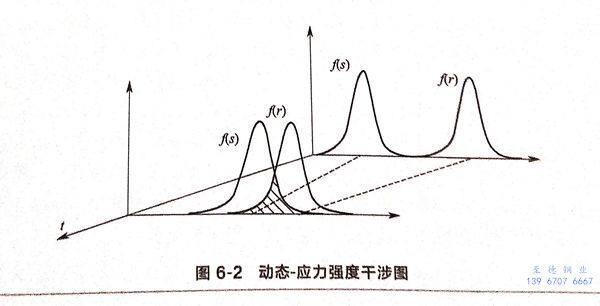
  大多(duo)數(shu)參數(shu)的不確(que)定(ding)性(xing)與(yu)時(shi)間(jian)有關。發生應(ying)力(li)腐(fu)蝕時(shi)，構件所(suo)受的廣(guang)義應(ying)力(li)一般是隨機過程，應(ying)力(li)稱為(wei)時(shi)間(jian)的函數(shu)，強度(du)為(wei)一固定(ding)的臨界值，如圖6-2所(suo)示，功能(neng)函數(shu)應(ying)表示為(wei)

二、應(ying)力腐蝕參數的概(gai)率分布估計(ji)

1. 變量(liang)分布類型(xing)確定

  采用(yong)S-R模型(xing)分(fen)(fen)(fen)析(xi)應力(li)(li)腐蝕(shi)(shi)失效(xiao)概(gai)率時(shi)，第一(yi)步是(shi)確(que)定應力(li)(li)腐蝕(shi)(shi)的“推(tui)(tui)動力(li)(li)”，即S所包含(han)的參(can)數(shu)，包括(kuo)溫(wen)度、侵(qin)蝕(shi)(shi)性(xing)離子(zi)濃度、pH值等(deng)，分(fen)(fen)(fen)析(xi)各參(can)數(shu)的分(fen)(fen)(fen)布(bu)概(gai)型(xing)。在(zai)進行參(can)數(shu)的概(gai)率分(fen)(fen)(fen)布(bu)類型(xing)研究中(zhong)，一(yi)般經過以下(xia)步驟：①. 假設隨機變(bian)量(liang)服從某(mou)一(yi)分(fen)(fen)(fen)布(bu)；②. 在(zai)假設分(fen)(fen)(fen)布(bu)基(ji)礎上構建統(tong)計量(liang)；③. 根據統(tong)計量(liang)的分(fen)(fen)(fen)布(bu)做出統(tong)計推(tui)(tui)斷，進行擬(ni)合檢驗；④. 選(xuan)擇最(zui)優概(gai)型(xing)。常用(yong)的統(tong)計量(liang)包括(kuo)均值、標準差、極(ji)差、變(bian)異系數(shu)、偏度等(deng)。正態分(fen)(fen)(fen)布(bu)、威布(bu)爾（Weibull)分(fen)(fen)(fen)布(bu)、指(zhi)數(shu)分(fen)(fen)(fen)布(bu)以及Poisson分(fen)(fen)(fen)布(bu)等(deng)都是(shi)應力(li)(li)腐蝕(shi)(shi)概(gai)率分(fen)(fen)(fen)析(xi)中(zhong)經常用(yong)到(dao)的隨機變(bian)量(liang)的概(gai)率分(fen)(fen)(fen)布(bu)類型(xing)。

通(tong)常，直(zhi)接(jie)計(ji)(ji)算概率(lv)的密度函數難(nan)度非常大，常用的處理方法是把概率(lv)密度估(gu)計(ji)(ji)轉化為參數估(gu)計(ji)(ji)問題。因此概率(lv)密度函數的確定是關鍵，正確的密度函數是獲得準確估(gu)計(ji)(ji)值的重要(yao)前提(ti)。

2. 參數(shu)的估計和假設檢驗

由于正(zheng)態(tai)分(fen)(fen)(fen)(fen)布情(qing)況發生的(de)(de)比較多(duo)，因此(ci)，以(yi)正(zheng)態(tai)分(fen)(fen)(fen)(fen)布為例加以(yi)說明。參(can)數估(gu)(gu)計(ji)(ji)的(de)(de)思路是(shi)采用(yong)(yong)樣本統計(ji)(ji)量估(gu)(gu)計(ji)(ji)總體(ti)參(can)數。常(chang)用(yong)(yong)的(de)(de)參(can)數估(gu)(gu)計(ji)(ji)方法(fa)有矩估(gu)(gu)計(ji)(ji)法(fa)和最(zui)大（極大）似然法(fa)，除此(ci)之外，還有最(zui)小二乘、貝葉斯估(gu)(gu)計(ji)(ji)等方法(fa)。矩估(gu)(gu)計(ji)(ji)法(fa)不受(shou)變(bian)量分(fen)(fen)(fen)(fen)布的(de)(de)影(ying)(ying)響(xiang)，這也恰恰成(cheng)為該方法(fa)的(de)(de)缺點，即(ji)變(bian)量的(de)(de)分(fen)(fen)(fen)(fen)布信息(xi)不能(neng)被充分(fen)(fen)(fen)(fen)利用(yong)(yong)，一(yi)般(ban)具有多(duo)個分(fen)(fen)(fen)(fen)析(xi)結果。與矩估(gu)(gu)計(ji)(ji)法(fa)相反(fan)，最(zui)大似然法(fa)的(de)(de)使用(yong)(yong)受(shou)已知(zhi)變(bian)量概型的(de)(de)影(ying)(ying)響(xiang)，必須(xu)在已知(zhi)概型的(de)(de)前提下(xia)才能(neng)使用(yong)(yong)，而(er)且假設(she)的(de)(de)概率模型正(zheng)確性(xing)對參(can)數估(gu)(gu)計(ji)(ji)結果影(ying)(ying)響(xiang)很大。最(zui)大似然估(gu)(gu)計(ji)(ji)法(fa)具有計(ji)(ji)算簡(jian)單、收(shou)斂型好等特點，在參(can)數估(gu)(gu)計(ji)(ji)中的(de)(de)應(ying)用(yong)(yong)更(geng)加廣泛，其主要計(ji)(ji)算步驟如下(xia)：

  式（6-10)稱為似(si)然方(fang)程(cheng)組(zu)(zu)，求解該方(fang)程(cheng)組(zu)(zu)，得出均值(zhi)、方(fang)差最大似(si)然估計(ji)值(zhi)

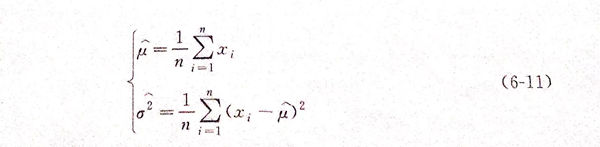
  以(yi)上過(guo)程是(shi)參(can)數(shu)(shu)(shu)估(gu)計，下面對(dui)參(can)數(shu)(shu)(shu)假(jia)設檢驗。與參(can)數(shu)(shu)(shu)估(gu)計的(de)目的(de)相同，參(can)數(shu)(shu)(shu)假(jia)設檢驗也是(shi)根據樣本信息(xi)對(dui)總體(ti)的(de)數(shu)(shu)(shu)量特征(zheng)進行推斷(duan)。

  假(jia)設(she)(she)檢(jian)驗(yan)(yan)是(shi)(shi)以樣本(ben)資料對總體(ti)的(de)先驗(yan)(yan)假(jia)設(she)(she)是(shi)(shi)否(fou)成立(li)，根據(ju)樣本(ben)的(de)統計(ji)(ji)(ji)量(liang)檢(jian)驗(yan)(yan)假(jia)設(she)(she)的(de)總體(ti)參(can)數的(de)可靠(kao)度(du)，同時做出(chu)判斷(duan)結(jie)果，判斷(duan)結(jie)果包括接(jie)受(shou)和拒絕。分(fen)析過程是(shi)(shi)：①. 提出(chu)原假(jia)設(she)(she)（要求(qiu)檢(jian)驗(yan)(yan)的(de)假(jia)設(she)(she)）H0 :F(x)=F0(x)和備選假(jia)設(she)(she)（如果原假(jia)設(she)(she)不成立(li)，就要接(jie)受(shou)另一個(ge)假(jia)設(she)(she)）H1:F(x)≠F0(x);②. 選取恰當(dang)的(de)檢(jian)驗(yan)(yan)統計(ji)(ji)(ji)量(liang)；③. 計(ji)(ji)(ji)算觀測值；④. 確定顯著性水平；⑤. 依據(ju)檢(jian)驗(yan)(yan)統計(ji)(ji)(ji)量(liang)觀測值的(de)位置給出(chu)判斷(duan)結(jie)果。

在以(yi)上(shang)分析過程中(zhong)，可能會犯(fan)(fan)兩(liang)類(lei)(lei)(lei)錯(cuo)(cuo)誤(wu)(wu)：當H0為真時(shi)(shi)而(er)(er)拒絕H0,稱為第(di)一(yi)(yi)類(lei)(lei)(lei)錯(cuo)(cuo)誤(wu)(wu)；當H0為假(jia)時(shi)(shi)而(er)(er)接受H0,稱為第(di)二(er)類(lei)(lei)(lei)錯(cuo)(cuo)誤(wu)(wu)。犯(fan)(fan)兩(liang)類(lei)(lei)(lei)錯(cuo)(cuo)誤(wu)(wu)的(de)概(gai)(gai)率(lv)(lv)(lv)通常是矛盾的(de)：一(yi)(yi)個概(gai)(gai)率(lv)(lv)(lv)小了另(ling)一(yi)(yi)個概(gai)(gai)率(lv)(lv)(lv)就大。在實際使用中(zhong)，我們一(yi)(yi)般限定(ding)犯(fan)(fan)第(di)一(yi)(yi)類(lei)(lei)(lei)錯(cuo)(cuo)誤(wu)(wu)的(de)概(gai)(gai)率(lv)(lv)(lv)不超過給定(ding)的(de)α,使犯(fan)(fan)第(di)二(er)類(lei)(lei)(lei)錯(cuo)(cuo)誤(wu)(wu)的(de)概(gai)(gai)率(lv)(lv)(lv)就可能小。在正態總體(ti)參數的(de)假(jia)設檢驗中(zhong)，主(zhu)要包括均值的(de)U檢驗和t檢驗、方差的(de)χ2檢驗等(deng)。

3. 分(fen)布的(de)假設檢(jian)驗(yan)

  上一小(xiao)節(jie)介(jie)紹的(de)(de)(de)是(shi)(shi)在總(zong)體分(fen)布(bu)(bu)已知的(de)(de)(de)情況下，對(dui)分(fen)布(bu)(bu)中(zhong)的(de)(de)(de)一些未知參數進行檢(jian)驗(yan)。但是(shi)(shi)，很(hen)多時候并不知道總(zong)體的(de)(de)(de)分(fen)布(bu)(bu)規律，我們往往是(shi)(shi)根(gen)據(ju)樣本來假設總(zong)體的(de)(de)(de)分(fen)布(bu)(bu)類型，因此，對(dui)于(yu)總(zong)體樣本所(suo)假設的(de)(de)(de)分(fen)布(bu)(bu)是(shi)(shi)否正(zheng)確，還需要檢(jian)驗(yan)，常(chang)用的(de)(de)(de)有χ2、J-B、A-D、K-S等檢(jian)驗(yan)方法，其(qi)中(zhong)χ2檢(jian)驗(yan)應用較(jiao)多，下面以(yi)這種方法為例，介(jie)紹檢(jian)驗(yan)過程(cheng)。

  χ2檢驗(yan)法的(de)分(fen)析過程是：①. 提出(chu)原假設(she)；②. 檢驗(yan)假設(she)H0:Fx(x)=F0(x;θ1,θ2,··,θm).先用若(ruo)干個互不相交的(de)小區間把樣本數據進行分(fen)組，通常每(mei)個區間的(de)數據不少于5個，若(ruo)不滿足(zu)這(zhe)一要(yao)求(qiu)，可以通過合(he)并區間來達到這(zhe)一要(yao)求(qiu)。假設(she)H0成立，根據分(fen)組結(jie)果(guo)計(ji)算χ2檢驗(yan)統計(ji)量(liang)

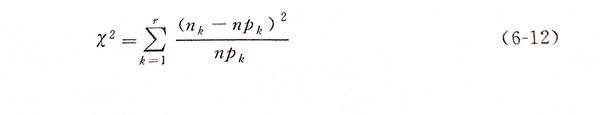
4. 主要參數的概率分(fen)布

 根據(ju)以(yi)上分析(xi)步(bu)驟，對應力腐蝕環境中的離子(zi)濃度(du)的統(tong)計性進行分析(xi)。數(shu)據(ju)來自某(mou)石(shi)化企業的監測數(shu)據(ju)。頻率直(zhi)方圖(tu)要將樣(yang)本(ben)值(zhi)分為r個不相交的區間，r值(zhi)可(ke)由(you) Sturges公(gong)式確定，并取整數(shu)。r值(zhi)取決(jue)于樣(yang)本(ben)數(shu)n。

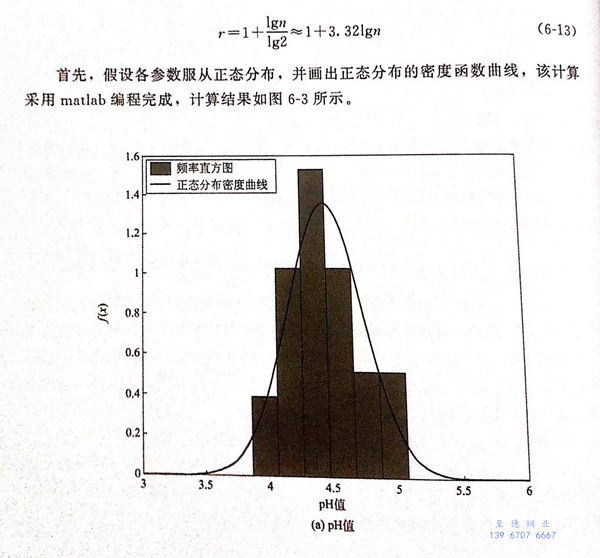
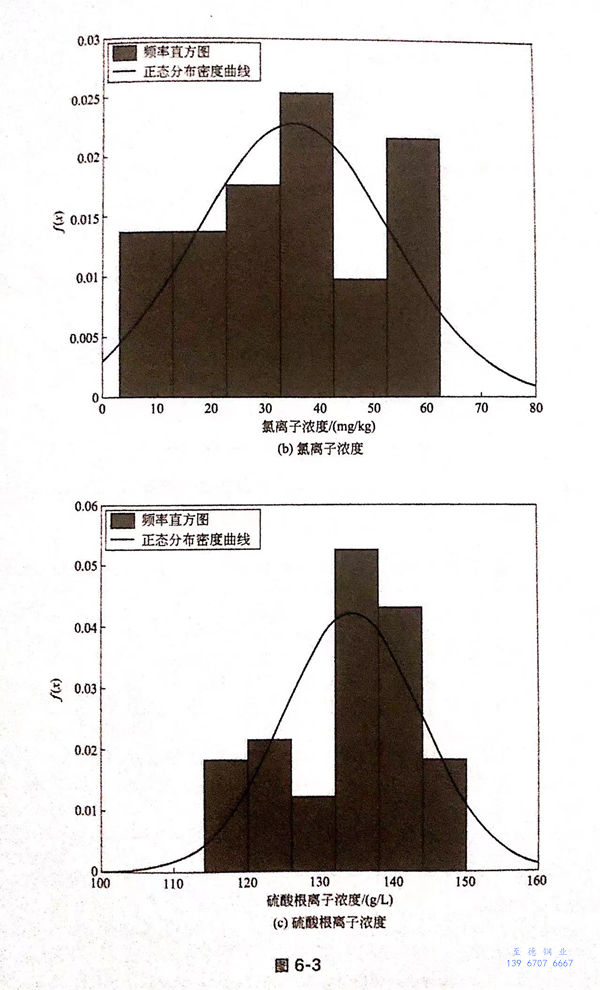
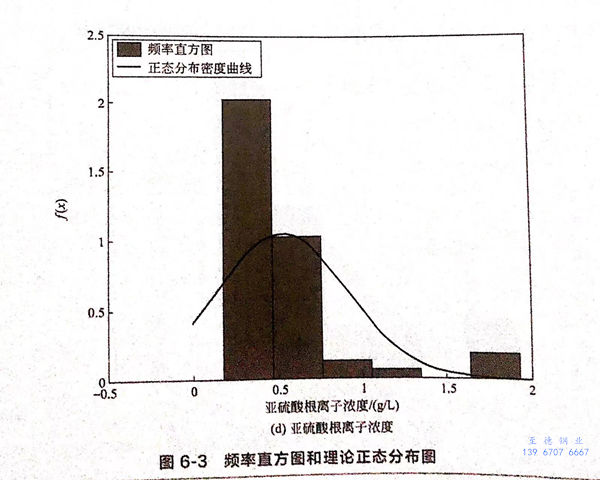
  首先，假設各(ge)參數服從正態(tai)分(fen)布，并畫出正態(tai)分(fen)布的密度函(han)數曲線，該計算采(cai)用matlab編程完成，計算結果如(ru)圖6-3所示。

  從圖6-3可以看出(chu)，pH、氯離子(zi)濃度(du)和硫酸(suan)根(gen)離子(zi)濃度(du)滿(man)(man)足正(zheng)態(tai)分布，而(er)亞(ya)硫酸(suan)根(gen)離子(zi)濃度(du)不滿(man)(man)足正(zheng)態(tai)分布，經過(guo)分析，認為滿(man)(man)足威布爾分布，如圖6-4所(suo)示。

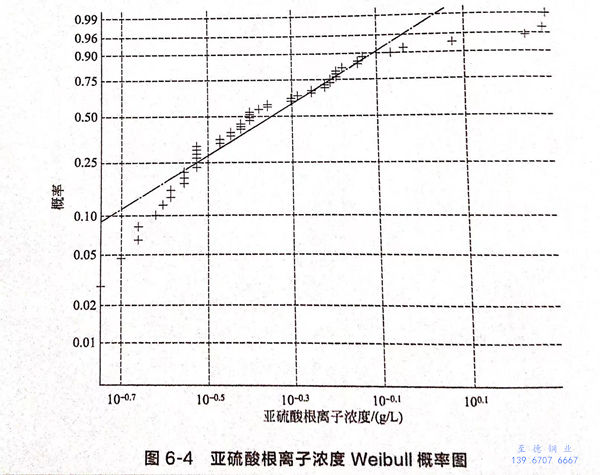
  經過卡方檢驗，在(zai)顯著性水平0.05下，可以(yi)認為：

  溫度(du)服從N(98.25,1.642);

  pH服從(cong)N(4.4608,0.29522);

  硫(liu)酸根離子濃度服從(cong)N(143.5204,9.48592);

  氯(lv)離子濃度服從N(35.3481,17.57352);

  亞(ya)硫酸(suan)根離(li)子濃度服從α=0.5926,β=1.5746的兩(liang)參數威布爾分布。

  亞硫(liu)酸(suan)根(gen)離(li)子濃度(du)服從威布爾分(fen)布的原因：亞硫(liu)酸(suan)根(gen)不(bu)穩(wen)定，與氫離(li)子反應，從而濃度(du)逐漸減小(xiao)。

三、失效概率(lv)計算方法

1. 解(jie)析法

  當應(ying)力(li)和強(qiang)度(du)是(shi)比較(jiao)簡單(dan)的(de)變量(liang)時，式（6-4)可以直接計算失效概率(lv)。在一些研究中(zhong)，會出現(xian)“干(gan)涉面積＝失效概率(lv)”的(de)說(shuo)法，這種(zhong)說(shuo)法是(shi)不(bu)正確的(de)。根(gen)(gen)據可靠性理(li)論可知，應(ying)力(li)－強(qiang)度(du)模型中(zhong)強(qiang)度(du)大于應(ying)力(li)的(de)概率(lv)即為可靠度(du)。可靠度(du)P可根(gen)(gen)據下式計算

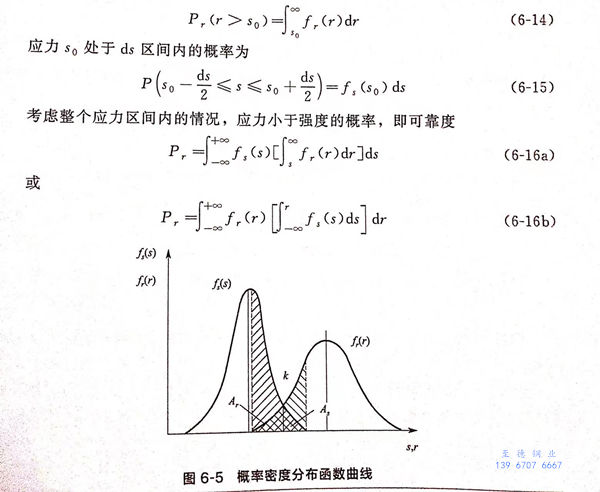
  從計(ji)算結果可以看出，失效概率遠小于干涉面積之和(he)。

2. 數值解析法

  當(dang)隨機(ji)(ji)變量(liang)較多(duo)時，直接求(qiu)(qiu)解(jie)(jie)失(shi)效(xiao)概率(lv)(lv)值是很困難的(de)，采(cai)(cai)用數(shu)值求(qiu)(qiu)解(jie)(jie)是一(yi)種(zhong)比較好的(de)解(jie)(jie)決方法(fa)(fa)。在應力腐蝕概率(lv)(lv)計算中(zhong)，涉(she)及(ji)的(de)隨機(ji)(ji)變量(liang)較多(duo)且(qie)具(ju)有不(bu)同的(de)分(fen)布類型，結果(guo)難以(yi)(yi)用解(jie)(jie)析法(fa)(fa)和近似法(fa)(fa)求(qiu)(qiu)解(jie)(jie)，可以(yi)(yi)采(cai)(cai)用蒙(meng)特(te)卡洛（Monte-Carlo)模擬(ni)法(fa)(fa)。Monte-Carlo模擬(ni)法(fa)(fa)的(de)特(te)點是：①. 受(shou)研(yan)究問(wen)(wen)題維(wei)數(shu)的(de)影(ying)響較小(xiao)；②. 不(bu)受(shou)假設約(yue)束(shu)；③. 不(bu)存在狀態空間爆炸問(wen)(wen)題；④. 不(bu)受(shou)變量(liang)數(shu)量(liang)的(de)影(ying)響。因此(ci)，Monte-Carlo法(fa)(fa)是一(yi)種(zhong)處(chu)理高(gao)維(wei)動態失(shi)效(xiao)概率(lv)(lv)問(wen)(wen)題的(de)方法(fa)(fa)。

  蒙特卡洛模擬(ni)法又稱為(wei)隨機模擬(ni)法，基本思想(xiang)是：