1. 圓盤波(bo)源縱波(bo)聲場

 在不(bu)考慮介質(zhi)中(zhong)衰減的情(qing)況下，圓盤(pan)波(bo)源(yuan)在理想液體(ti)介質(zhi)中(zhong)振動(dong)輻射聲波(bo)，其中(zhong)某(mou)一點(dian)波(bo)源(yuan)d,在波(bo)源(yuan)軸線上Q點(dian)所(suo)引起的聲壓為（圖2.13)

基于波的疊加(jia)原理，整(zheng)個(ge)圓盤波源上(shang)各點(dian)在Q點(dian)引(yin)起的聲(sheng)壓(ya)疊加(jia)，就是Q點(dian)處的聲(sheng)壓(ya)，由此可得到軸線上(shang)任(ren)一點(dian)的聲(sheng)壓(ya)幅值為

波源軸線上的(de)聲壓隨距離(li)變(bian)化(hua)的(de)情況如圖2.14所示。

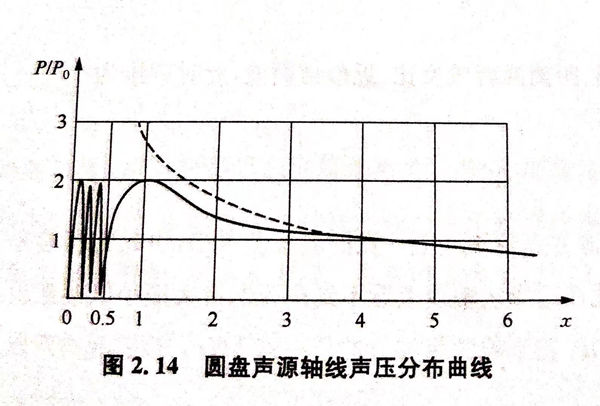
 由于(yu)波的干涉，在波源附(fu)近(jin)區(qu)域會出(chu)現一系列(lie)聲壓(ya)極(ji)大(da)極(ji)小(xiao)值，這片區(qu)域稱為近(jin)場(chang)區(qu)，也(ye)稱菲涅爾區(qu)（Fresnel).在近(jin)場(chang)區(qu)由于(yu)波源上(shang)各點到軸(zhou)線上(shang)某一點的距離不同(tong)，存在波程差，互(hu)相(xiang)疊加(jia)時存在相(xiang)位(wei)差，出(chu)現互(hu)相(xiang)干涉，進而出(chu)現聲壓(ya)極(ji)大(da)極(ji)小(xiao)值點。

波源到波源軸線(xian)上(shang)最后一個聲(sheng)壓極(ji)大(da)值(zhi)(zhi)間(jian)的距離稱為(wei)近場區(qu)長(chang)度(du)，常用N表示。由(you)軸線(xian)上(shang)任一點(dian)的聲(sheng)壓幅值(zhi)(zhi)公式進一步化簡(jian)可(ke)得(de)極(ji)大(da)值(zhi)(zhi)出現的位(wei)置為(wei)

在近(jin)場區檢(jian)(jian)測(ce)(ce)容易引起(qi)誤(wu)判(pan)，甚至漏檢(jian)(jian)，因(yin)此探傷過程中盡可(ke)能避免在近(jin)場區檢(jian)(jian)測(ce)(ce)。

波源軸線上一點到波源距(ju)離(li)(li)大于N的(de)區域稱為(wei)遠場區，又稱弗(fu)朗合費區（Fraunhofer)。遠場區軸線上的(de)聲(sheng)壓(ya)隨距(ju)離(li)(li)增加而單調(diao)遞減。當x大于3N時，聲(sheng)壓(ya)、距(ju)離(li)(li)兩者成反(fan)比(bi)，近似球面(mian)波，此時聲(sheng)壓(ya)為(wei)

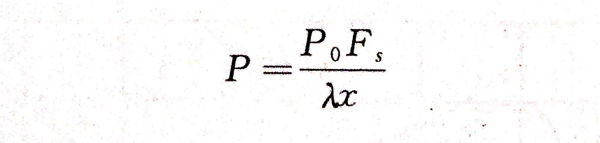
這時波(bo)源(yuan)各點(dian)到軸線(xian)上一點(dian)的(de)(de)(de)波(bo)程差很(hen)小，引起的(de)(de)(de)相位差也很(hen)小，干涉(she)非常小，因(yin)此在遠場區(qu)軸線(xian)上看不(bu)到聲壓的(de)(de)(de)極大(da)極小值接連出(chu)現的(de)(de)(de)現象。

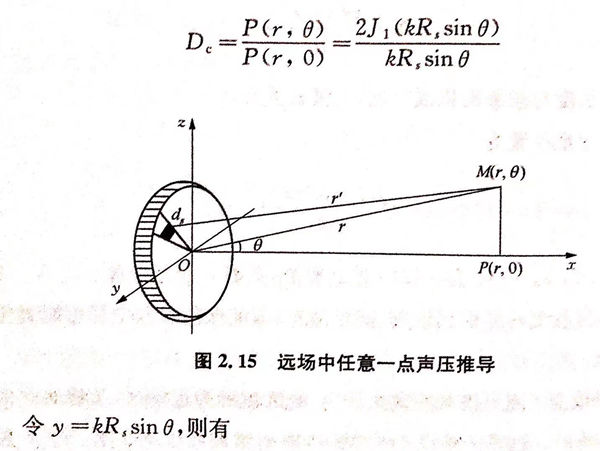
點波源d_s在到波源足夠遠的任一點M(r,θ)引起的聲壓為

圖2.15中(zhong)點(dian)M(r,θ)與波源軸線上同距離處聲壓P(r,0)之比，稱為指(zhi)向性(xing)系(xi)數(shu)，常用(yong)D.表示(shi)：

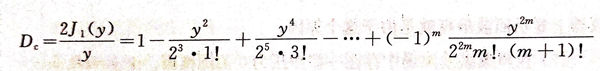
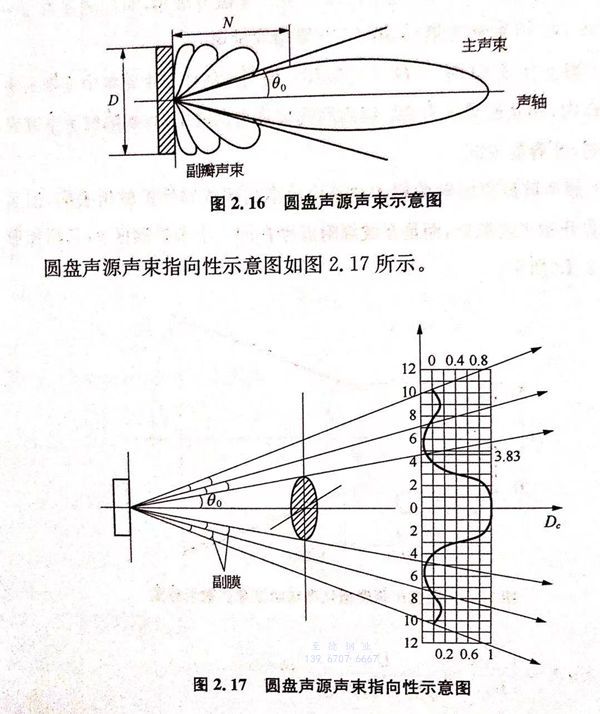
 從圓盤(pan)(pan)聲(sheng)(sheng)(sheng)(sheng)源(yuan)出發，聲(sheng)(sheng)(sheng)(sheng)源(yuan)所輻射的(de)能量集(ji)中在(zai)一定(ding)區域內，以束(shu)狀傳播(bo)，稱(cheng)為(wei)(wei)聲(sheng)(sheng)(sheng)(sheng)束(shu)的(de)指(zhi)向性。用聲(sheng)(sheng)(sheng)(sheng)束(shu)邊緣線(xian)與軸線(xian)之間(jian)的(de)夾角(jiao)(jiao)來評價聲(sheng)(sheng)(sheng)(sheng)束(shu)指(zhi)向性好壞，這個夾角(jiao)(jiao)稱(cheng)為(wei)(wei)半擴(kuo)散角(jiao)(jiao)，常用θ表示(shi)。圓盤(pan)(pan)聲(sheng)(sheng)(sheng)(sheng)源(yuan)聲(sheng)(sheng)(sheng)(sheng)束(shu)如圖2.16所示(shi)。

由圖2.17可知：

a. 在(zai)聲源軸(zhou)線(xian)上某(mou)一(yi)點(dian)到聲源的距離足夠遠時，這(zhe)一(yi)點(dian)所在(zai)橫截面上各點(dian)的聲壓(ya)是(shi)不同的，且以軸(zhou)線(xian)上聲壓(ya)最高(gao)。當缺陷與波束軸(zhou)線(xian)垂直時，儀器上顯示回波最高(gao)就是(shi)由(you)于這(zhe)個原因。

b. 在聲(sheng)束縱波聲(sheng)場中存在一些聲(sheng)壓為0的圓錐面。由y=kR，sinθ=3.83 可得(de)

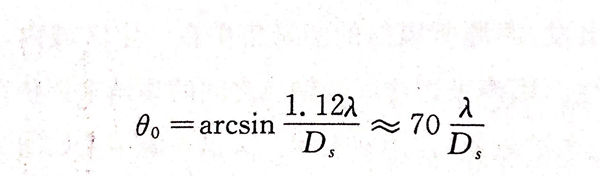
此的θ₀ 稱為第一半擴散角，也稱第一零值發散角，對應的還有y=7.02,10.17,···時稱為第二、第三、···零值發散角。

c. 當y>3.83時，｜D_c |<0.15.說明聲波能量主要集中于第一半擴散角以內，因此通常認為2θ₀ 以內的波束稱為主波束，當缺陷位于主波束范圍內時，才容易發現。

d. 超(chao)聲波波源輻射的(de)(de)超(chao)聲波是(shi)以聲束的(de)(de)形式(shi)向外擴(kuo)散(san)(san)出去的(de)(de)，但實際上并(bing)非開始(shi)于波源處(chu)，而(er)是(shi)在波源附近(jin)存在的(de)(de)一個(ge)未擴(kuo)散(san)(san)區b,其理想形狀如圖2.18所示(shi)。

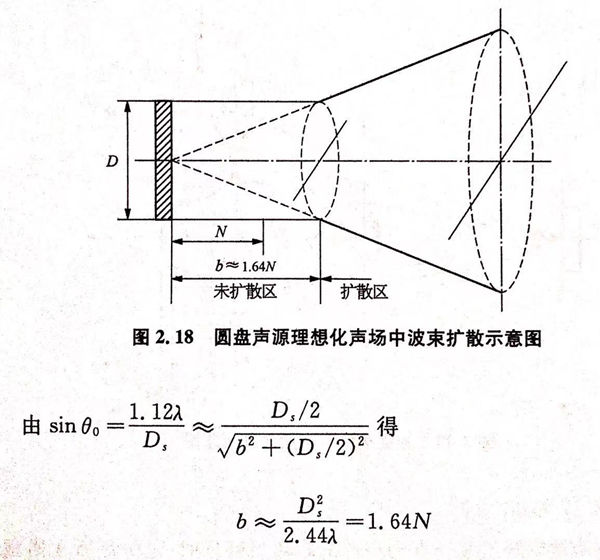
距離(li)波源大(da)于b的區(qu)(qu)域(yu)成為擴散區(qu)(qu)，波束在(zai)擴散區(qu)(qu)中會逐(zhu)漸衰減。

2. 矩形波源縱(zong)波聲場(chang)

矩形(xing)波(bo)源(yuan)(yuan)振動時在(zai)理想液體介質(zhi)中(zhong)的(de)縱波(bo)聲(sheng)場(chang)與圓盤(pan)波(bo)源(yuan)(yuan)一樣有近(jin)場(chang)區和未(wei)擴散角等。但(dan)是在(zai)近(jin)場(chang)區內聲(sheng)壓分布比(bi)圓盤(pan)聲(sheng)源(yuan)(yuan)更為(wei)繁(fan)雜(za)，計算困(kun)難，其遠場(chang)區聲(sheng)源(yuan)(yuan)軸(zhou)線上任(ren)一點(dian)Q(r,0,φ)處的(de)聲(sheng)壓可以(yi)通過液體介質(zhi)中(zhong)的(de)聲(sheng)場(chang)理論推導出來，如下：

所(suo)以矩形波(bo)源(yuan)發出的(de)縱波(bo)聲(sheng)場(chang)與圓盤聲(sheng)源(yuan)不同，具(ju)有兩個不同的(de)半(ban)擴散(san)角，聲(sheng)場(chang)為矩形。